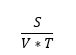VFR Navigation
Home >> Aviation Guides >> VFR Navigation VFR, or Visual Flight Rules, is flying & navigating by terrain, landmarks or other visual features outside the aircraft. This guide is intended to help new players with mastering this skill. The guide is divided into three parts - Navigation basics, Flight planning and Follow-up during flight. Flight planning is the planning performed before starting the flight, and follow-up covers methods for continuously verifying that you are where you are meant to be once underway.
The most basic form of VFR Navigation consists of looking outside the aircraft and using landmarks together with a map to navigate. This method requires relatively little preparation but can be perfectly accurate if sufficient landmarks are present in the terrain you're flying over. See section 'follow up during flight' for tips on referencing your position in regards to visual landmarks. For flights over terrain where visual landmarks are few and far inbetween, such as large bodies of water, different methods and more thorough preparation may be required to successfully navigate.
Innehåll
Speed terms
There are several different methods for qualifying an aircraft's speed relative to the air Indicated Air Speed (IAS) is the uncorrected speed which is displayed on an aircraft's airspeed indicator. Multiple factors affect either the air itself or the airspeed instrument causing this airspeed to, genereally speaking, not actually match the aircraft's speed true speed relative to the air. The main error sources are Instrument error (Errors due to the construction / design of the cockpit instrument), Position error (When the positioning of the Pitot tube causes the pressure reading from which the airspeed is calculated to be inaccurate) and Density error (The airspeed instrument is calibrated for standard sea-level density, meaning that it will get less and less accurate as the measured air density decreases with increased altitude)
Calibrated Air Speed (CAS) is the IAS but corrected for instrument and position errors. In real life the airplane manufacturer provides the pilot with the information required to convert IAS to CAS. In DCS this information is rarely inlcuded in manuals - if no information is provided, assume that IAS = CAS.
EAS - Får gärna fyllas i av någon IRL-jet-nörd. Mvh// Flyger-aldrig-över-115-knop
True Air Speed (TAS) is a measure of the aircrafts true speed relative to the air. This is calculated by taking the CAS and correcting for the density error. Some DCS aircraft provide you with the TAS automatically. Calculating the TAS manually can be done with a flight computer (see Resources heading at the bottom). Calculating your TAS manually requires known values for pressure altitude, which is simply the reading on your barometric altimeter with QNH entered as well as the outside air temperature (as the density of the air for a given altitude varies depending on the temperature). The temperature in DCS is generally speaking only given for sea level, so to calculate the temperature for a given altitude use the ISA standard temperature change of 2°C / 1000 feet or 6,5°C per 1000 Meters. ¨
E.g. - if the Sea level temperature is +18°C and you're planning to fly at 8000 feet, the expected change in temperature is 2°C * 8 = -16°C. The outside air temperature is thus +2°C.
Ground speed (GS), is the actual speed your aircraft is travelling relative to the ground. This is important for navigating as it is this speed we will be using for calculating how long it will take to fly our waypoints later. Ground speed is calculated by taking the true air speed and correcting this for wind. This calculation can be performed using a flight computer or the online E6B tool linked in the resources section.
To perform the calculation, start by entering the true course in the course field. Enter the True Air Speed in the next field. Enter the Wind direction (Where the wind is coming from) and the wind speed and read the wind correction angle below. This angle is the amount of degrees you'll have to add or subtract from your course in order to compensate for wind. You'll now be able to read the ground speed below the Wind correction angle.
Note 1: Since the only source of variation between TAS & GS is the wind, TAS & GS will be equal if flying with no vind Note 2: In DCS, unlike in real life, the wind strength and direction is constant within the same mission. You will still need to calculate the wind correction angle for each leg as the heading of your aircraft relative to the wind affects the WCA.
Course terms
Courses are given relative to one of three sources - True (Relative to the geographic, or true, north pole), Magnetic (Relative to the magnetic north pole) or compass (Relative to the north pole of the magnetic field which the compass is picking up). In real life compass north deviates from magnetic north due to metallic objects in the airplane interfering with the magnetic field of Earth. To my knowledge this is not modelled in DCS, so focus on understanding True and Magnetic.
Different terms are used for describing various angular differences. Track is the angular difference between two points on the map. True track is defined using true north as a reference and Magnetic Track is defined using Magnetic north.
Heading, or course, is the angular difference between your chosen source of reference and which angle your aircraft is currently pointing.
Bearing is the angular difference between your aircraft and another object - aircraft, bullseye, terrain or something else. True bearing is relative to true north and magnetic bearing is relative to magnetic north.
Wind correction angle
Calculating the WCA is covered in the speed terms section above.
Compass Magnetism
North on most maps is pointing directly towards the geographic north pole. North on an aircrafts magnetic compass is pointing towards the magnetic south pole, which is actually located in the northern hemisphere. The Geographic North Pole and the Magnetic South Pole are not located at the same point, meaning that a compass will not point to true north. The difference between true north and magnetic north for a given location on Earth is called variation and is expressed in either degrees west / east or degrees +/-. The variation for Caucasus is +6°, or E6.
When we make our flight plans using the F10 map we are plotting tracks in relation to true north, but when we then fly these headings (assuming your aircraft isn't displaying true north) you are using magnetic north. You must therefore add or subtract the variation to the magnetic course reading in order to correct for the variation.
For example, if you're flying a waypoint leg in Caucasus with True Track = 360° and Variation is +6°, you should make fly a magnetic course 354° to compensate.
Magnetic variations for the current maps are: Caucasus: +6° Persian Gulf: +2° Normandy: +1° Syria: +5°
Coordinates
Latitude is the amount of degrees a given point is north or south of the equator. Ranges from 0-90° North and 0-90° South. Longitude is the amount of degrees a given point is east or west of the prime meridian, i.e. Greenwich, UK. Ranges from 0-180° East & West.
Each degree is divided into 60 Arc minutes (designated ') and each arc minute is further divided into 60 arc seconds (designated "). A coordinate of N40°42'13" thus means North 40 degrees, 42 arc minutes & 13 arcseconds.
Along a great circle (a circle along the earth that splits the planet into two equal parts, i.e. a circle that passes through the centre of the earth. All meridians and the equator are great circles, but any latitude parallell to the equator is not) one arc minute equals one nautical mile, or 1852 meters. One arc second thus represents, along a great circle, 30 meters (1852/60) or 98 feet. This is our accuracy when using this coordinate format, well within acceptable margins for VFR navigation.
Time, speed and distance calculations
Calculating the time to fly a leg, the distance of a leg or the speed required to fly a leg of a given distance at a given time is made easy wit the SVT-triangle. S stands for Sträcka (Distance), V stands for Velocity (Fart) and T stands for Tid (Time). For as long as two values are known, the third is calculated using the formula in the image below. Simply remove the variable you want to solve for and follow the formula for the remaining two.
Examples: If S = 300 NMI and V= 415 knots, what is T? (How long does it take to fly a given distance at a given speed) Answer: We remove T and find that the formula now states S/V. 300/415 = 0,722. This is the time required expressed in decimal format. To convert this to hours:minutes, simply carry over the hours and multiply everything right of the decimal with 60. 0,722 * 60 = 43,32. Note that the seconds are still presented in decimal format, so once again we multiply the seconds right of the decimal with 60 and get 0,32*60 = 19,2 (Round to the nearest second). Flying this leg will take zero hours, 43 minutes and 19 seconds (00:43:19).
If S = 25 NMI and T = 15 minutes, what is V? (Which speed do I have to maintain to fly a given distance at a given time) Answer: First convert 15 minutes to decimal format. Again we carry over the hours but we now divide everything right of the decimal with 60. 15/60 = 0,25. We can now perform the speed calculation. Remvoing V the formula now says S/T. 25/0,25 = 100. To fly this leg in 15 minutes we require a ground speed of 100 knots.
If V = 215 knots and T = 25 minutes, what is S? (If I fly a given speed at a given time, how far will I travel? Answer: Again we convert time to decimal - 25/60 = 0,416. Solving for distance we remove S from the triangle and find the formula to be V*T. 215*0,416 = 89,44. We will travel 89,44 nautical miles in 25 minutes at 215 knots.
Practice questions
1. If S = 73 and V = 215, what is T?
2. If S = 428 and T = 01:15:00, what is V?
3. If V = 317 and T = 00:45:30, what is S?
Another method for calculating flight times is the speed factor method. If you're travelling at 60 knots, you're travelling 60 nautical miles per hour or 1 nautical mile per minute. This is also known as speed factor 1. 120 knots is speed factor 2 (2 NM/Minute), 600 knots is speed factor 10 (10 NM/Minute) and so on.
Flight planning
Start by marking your initial point and your destination on the map. Continue by marking waypoints along the route at reasonable intervals. These waypoints act as control points, allowing you to verify that you are flying where you've intended and allowing you to correct and errors before they accumulate too much. I would recommend no more than 20NMI between each waypoint. Generally speaking, shorter legs makes it less likely that you'll get lost, but will also mean that more work is required during the planning phase.
Once you have all your waypoints marked, plot the true track between them. This is the true track. Enter this into your flight plan for each leg. Now add or subtract the magnetic variation to get the magnetic track for each leg. Decide upon a desired altitude for each waypoint.
Next we'll be calculating the magnetic heading, i.e. the course you will be aiming for when flying. Start by deciding upon a certain IAS you want to use for your flight. You can alternate different IAS for different legs to make it more challenging. Once you have that IAS, carry it over to CAS and use that in combination with the outside air temperature and waypoint altitude to calculate your TAS. Now use your CAS and use that in combination with the true track & wind information to calculate your wind correction angle and your ground speed. This step will have to be re-done for every waypoint leg (assuming the track is different between them).
For each individual leg, add or subtract the wind correction angle to the magnetic heading and enter the ground speed into your flight plan. Use this ground speed to calculate how long it will take to fly the leg (leg time) as well as an accumulated total time (the sum of all leg times up to that waypoint).
This is all the core information you require to succesfully navigate from point A to B without crutches such as GPS, NDBs, Tacan etc. Remember that the better and more thorough your flight plan, the easier it will be to perform the flight once in the aircraft.
This guide has not covered control points. These are not proper waypoints but points of interest along your track which are meant to help you verify that you are on-track, such as a bridge, lake or other geographic feature easily seen from the cockpit. I generally find that these aren't required for a waypoint interval of roughly 20nm, but depending on the terrain these may still be a good idea. To add a control point to your flight plan, first measure how far into the leg you should cross it. If you for example cross a bridge 40% of the distance between WP1 and 2, you should reasonably expect to cross that bridge after 40% of your leg time has elapsed. Add the control point to your flight plan and note at which time you ought to fly over it. If during the flight you notice that you're 30 seconds late with flying over the bridge you need to increase your speed a bit to compensate for the rest of the leg.
It is possible (and recommended) to set your start waypoint in the air rather than at take-off. This will mean that you can be at your set altitude, course and speed immediately after passing the start waypoint, which makes it far easier to calculate ETA.
Example Flight plan
| Waypoint | Latitude | Longitude | Description | True Track | Magnetic Track | Magnetic Heading | Distance | Leg time | Total Time |
|---|---|---|---|---|---|---|---|---|---|
| Start | N42°11’58” | E42°42’02” | Railroad bridge, east of Kutaisi Exit east | 270 | 264 | 268 | 20,8 | 00:05:00 | 00:05:00 |
| 1 | N42°06’33” | E43°02’42” | Road bridge, just south of a railway crossing | 243 | 237 | 241 | 21,4 | 00:07:30 | 00:12:30 |
Follow-up during flight
Always try to be one step ahead. If you know that your next waypoint is located above a television mast, try to locate the mast as soon as you can. Once you've located it, mentally mark it's position and start looking for your next waypoint. It's always easier to stay on track than to find your way back after getting lost, so try to always look out the cockpit for geographical features or other landmark and reference your position in relation to these.
Two landmarks can be used together to determine your position with reasonable accuracy. Estimate the bearing from the first landmark to you, and do the same for the second landmark. Now draw an actual (or imaginary) line on the map with that bearing originating at each landmark. You should be roughly where those two lines intersect.
Calculating drift
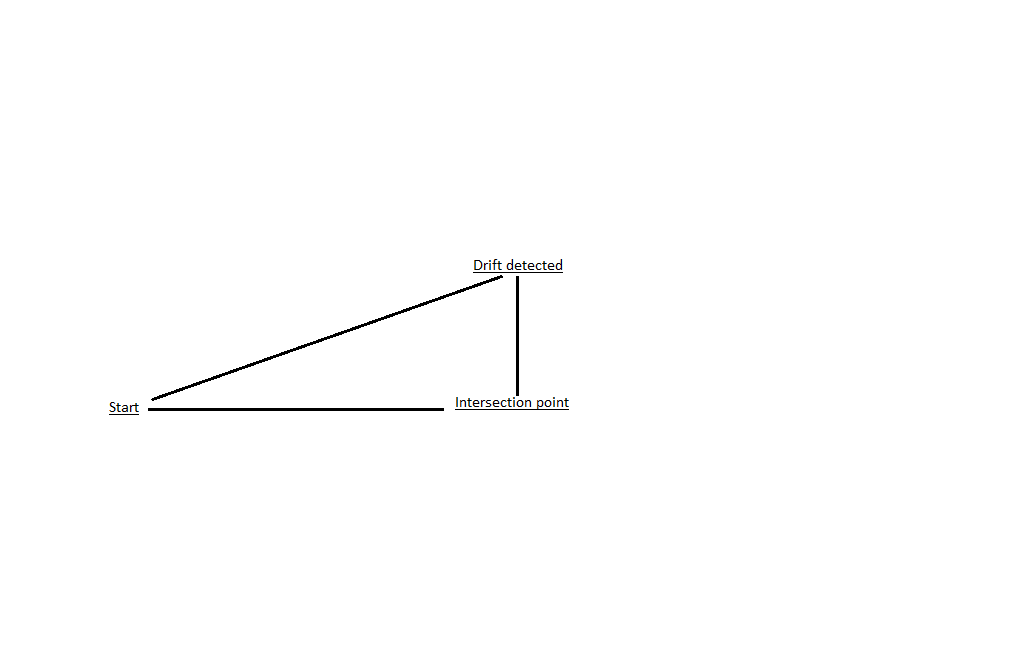
A handy method for calculating the degrees you've drifted off the track is via trigonometry. Imagine the track being the leg adjacent to the angle and the drift distance being the leg opposite the angle of a right triangle. If we know the values for these we can calculate the angular difference, i.e. the angular drift off the track.
I won't go in to detail in how this works, but the short version is that the relationship between the angle and length of the legs in a right triangle means that if the adjacent leg is 60 units long & the opposite leg 1 unit long the angle will be 1°. If the legs are 60 units / 5 units the angle will be 5° and so forth. Note that the unit used doesn't matter as the relationship still applies.
First find your current position on the map. Now draw a line that intersects with the track line at a 90° angle. We now have the length of both the adjacent and opposite legs. Now try to get the adjacent leg to 60 by multiplying or dividng it, and then multiply or divide the opposite leg using the same factor. If the near leg is 60, the opposite leg will equal the amount of units off the track and the angle will equal the amount of degrees off track.
Example: You notice that you've drifted off course and find your position on the map. You then draw a line from this position to the track line. You find that the distance along the adjacent leg from the start point to the intersection point is 15 nautical miles, and the distance from your current position to the intersection point to be 0,5 nautical miles. How many degrees off course are you?
Answer: Multiply the adjacent leg so that it equals 60, in this case 15*4. Now multiply the opposite with 4 as well. With the adjacent leg being 60 and the opposite leg being 2, we can use the relationship described above to determine that we've flown 2 degrees off course.
This method is called the 1 in 60-rule (Sv. 1 på 60-regeln).
Correcting for drift
Continuing with the example above, we've detected ourselves as having flown 2 degrees too much to the left and are now 0,5 nautical miles off our track. The easiest way to correct for this is to multiply the error with two and change your course with that amount in the opposite direction.
For example, if our original track was 150° and our course, after calculating for wind drift was 148, we multiply two by two and add that to our course, making our course 152°.
This will mean that the time to return to the track will roughly equal the amount of time we spent off the track. Once you are back on track, you stop over-compensating and return to course 150°. This method depends on knowing roughly or at least estimating when you started drifting.
If the drift is noticed after passing the halfway point of your waypoint leg and the drift started early on, this method no longer works as you would end up back on track after passing your waypoint (by which point the track is likely to have changed). In these cases you will need to estimate an angle larger than your drift angle.
A more precise method comes via using the 1-in-60-rule again. For example, you're track is 40 nautical miles long. After flying for 15 NMI you notice that you are off-track and use the method outlined in the previous chapter to determine your off-track angle. In our example you find yourself 2 nautical miles north of the track.
First, calculate the angle off track: 15*4 = 60 2*4= 8
We're 8 degrees off track.
As the remaining track distance also forms a right triangle with our current position, we can use that to calculate how many degrees we need to turn in order to correct for the earlier drift.
As our total track was 40 NMI long and we've flown 15 when we discovered the drift, we've got 25 nautical miles left. Again we need to multiply this number so that is becomes 60. 25*X = 60 -> X= 25/60 = X = 0,416. We now divide both the track and the distance off track with this number. 25/0,416 = 60. 2/0.416 = 4,8
4,8 (round to 5) is in relation to the track, so if you add that to your desired track you should end up over your waypoint.
Since the wind in DCS is static, i.e. it doesn't change once a mission has been started, the most common source of drift is poor and/or faulty planning. To avoid having math interfere with your flying always make sure that your wind correction angles are propely calculated during the planning phase.
Suggested exercises
Basic exercise
This exercise doesn't require many of the topics in this article. You just fly headings and look out the window.
The following route should be flown in clear weather at 3000 feet without steerpoints, tacan or moving map. You are not allowed to use the in-game map if it shows your current position. You will need to write down headings, approximate distances and landmarks.
- Take-off Kutaisi
- Zugdidi city
- Poti city
- Land Kutaisi